前回の記事:平均と中央値
前回の最後で「次回は偏差値になるかも」と書きましたが、 全然アイデアが出てこないので、その通りになりました。
偏差値の求め方なんて仕事に役立つのか分かりませんが、 分散と標準偏差の概念は覚えられるので、これで勘弁してくだち。
長くなりそうなので、無駄話は省いて極力説明だけにしていきます。
偏差値の求め方
下表のようにAさんからNさんの14人が英語のテストを受けた場合の、各人の偏差値を求めます。 (当初は10人にしていたが、少ないので増やした。ちなみに原稿は10人のままで、それに気付いたのは3日後)
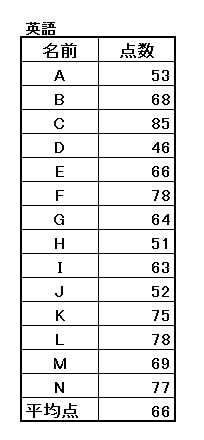
1.まず平均を求めます。
2.次に「分散」を求めます。
3.分散の平方根から「標準偏差」を求めます。
4.各点数を偏差値の式、(点数−平均点)/標準偏差 ×10+50に当てはめて、 偏差値を求める。
すると下表のように各人の偏差値が定まります。簡単でしょう。
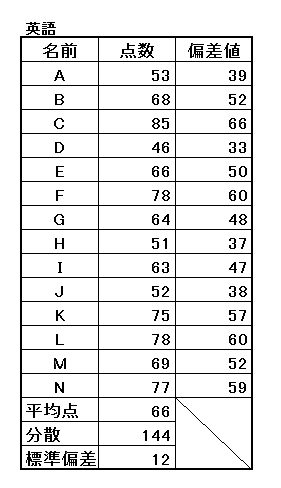
分散と標準偏差って何だ

各点数と平均点との差を2乗し、2乗した14個のデータを全て足す。それをデータの個数14で割ったもの。
まず分散についてですが、分散とは上のような式で、 要するに「全データの散らばり具合」を示す数字だと思ってください。
分散の式を図形的に示すと、下図のように1辺の長さが「平均点との差」の正方形があり、 各正方形の面積の平均が「分散」というわけです。
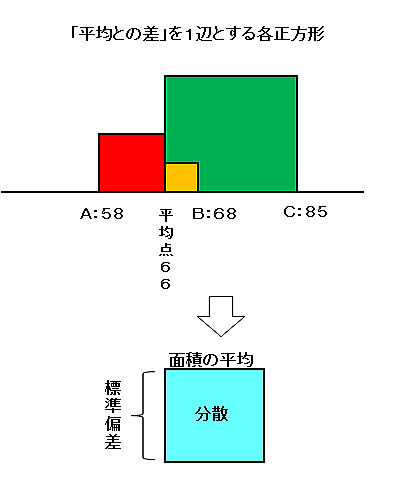
本当は正方形が14個あるのだが、面倒なのでA~Cまでの3つ。標準偏差の2乗が分散となる。
また、分散(正方形の面積)の1辺の長さが「標準偏差」となり、
よって標準偏差=√分散ということになります。
ヒストグラム(正規分布)とかやれば標準偏差は意味ある数字なのですが、 私に説明できる力量が無いので割愛します。
偏差値の式の意味
偏差値の式はこのようになるのですが、 統計的に意味があるのは(点数−平均)/標準偏差の部分だけです。 他の部分については以下の様な感じ。

×10の意味:「+1.3とかよりも+13の方がインパクトあるから」という下らない理由。
+50の意味:「-1.5とか-15だと生徒が可哀想だから」という下らない理由。 平均点と同じ点数なら偏差値50になるのはこのため。
ともかく、(点数−平均)/標準偏差についてですが、 何で分散でなく標準偏差で割るのかというと、上の分散と標準偏差の図で見たように、 分散=面積、標準偏差=辺みたいな感じです。
分子が「点数−平均」という直線の次元なので、それを面積で割る(面積と比較する)のはおかしいだろう、 割るなら分子と同じく直線だろうということで、標準偏差というわけです。
要するに偏差値とは、上図にある「”14個の(3つしかないけど)各正方形の1辺”と、 ”平均的な正方形(分散)の1辺”とを比較している」ということなのですが、 私が説明できるのはここまでで、その他一切のことはわかりません!
この辺詳しく知りたい方は、 こんなサイト見るより自分で統計学を勉強してください。
最後に、Excelでの標準偏差はSTDEV関数、平方根はSQRT関数です。 分散は標準偏差を2乗して求めましょう。
次回はこれらを実際に職場で使用する場合について書いてまいります。
分散と標準偏差を職場で使うに続く。
生きる上で大変ためになる記事一例
引き寄せに関する大変素晴らしい記事一例
...