前回の記事:偏差値の求め方、分散と標準偏差
前回の続きで、今回は「分散や標準偏差を職場で使っちゃおう」 という内容なのですが、
特に新しい知識などは無く、下らない雑談に終始いたします。
分散を使う
まずは分散についてです。分散とは「バラつきを示す数字」なので、 どちら(どれが)が安定しているかを説明するのに使えます。
例えば下記のような中古のマシニングセンタが2台あり、 値段は同じ1000万円だったとします。テストを14回おこなった精度は以下の通り。
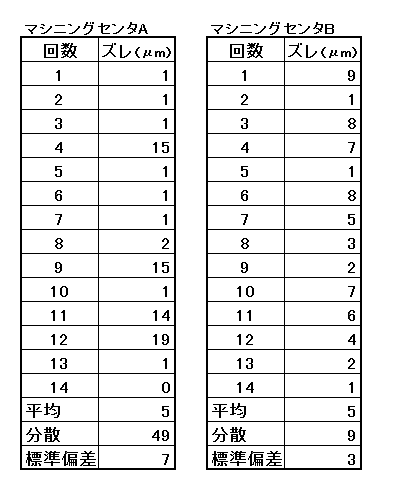
都合上、精度がガバガバ
この場合どっちを選ぶかですが、統計を用いて説得するなら、 「Aの分散が49に対し、Bの分散は9なので、Bの方がバラつきが少なく精度が安定しているといえます」 なんてことが言えるわけです。 (ちなみに平均は同じ。平均が同じでも分散が異なることはよくある)
でも、Bを購入したら直後に動力源から火が出ておジャンになったとか、 Aの方がメンテ後に精度が出るようになりAの方が良かったとか、 実際に使ってみないと分かりません。
こんなことなら「どちらにしようかな天の神様の言うとおり」で選んだ方がマシなのですが、 それだと他人を説得できないから、仕方なしに統計というものを用いるのです。
ちなみに私が選択を迫られた場合は、 10円玉を投げて決めますし決めてまいりました。
標準偏差を使う
次に標準偏差についてですが、前回説明した「(値−平均)/標準偏差」の値を 平均の代わりに使うのが一番おススメです。
「この値は平均より何ポイント高い」なんて説明するよりも、 「この値は標準偏差を用いれば+1.5σ(シグマ)である」なんて言った方が、 説明を受けている方は何のことか分からず、 「理解できないもの=凄いもの」みたいな目眩ましになるからであります。
分かりやすくしたいなら、各値を10倍して50を足して偏差値に変換し、 「皆さんご存知の偏差値に変換すると…」みたいな感じで説明すれば良いでしょう。
使うときの注意
最後に、これらの知識を使うときの注意なのですが、 私の様に大学等で統計学を学んだことない人間は、 こんなのはあくまで付け焼き刃の知識に過ぎないので、 説明する相手が統計やその周辺に疎いことを確認してから使いましょう。
とはいっても、1部上場企業でも研究開発部門以外はまずこんなの使わないので、 大丈夫といえば大丈夫なのですが、たまに詳しい人間がいたりするので油断できません。
社外でなく社内の人間を説得するのに限定して使用した方が無難です。
次回は(気が向いたら)単回帰分析について書いてまいりますが、何の事はない1次関数を用いて 「既存のデータがこうだから将来こうなるだろう」と予想するみたいなものです。
単回帰分析を使うに続く。
生きる上で大変ためになる記事一例
引き寄せに関する大変素晴らしい記事一例
...