前回の記事:分散と標準偏差を職場で使う
前回の予告通り、今回は単回帰分析について適当に書きます。
本当に適当に書くので、統計学とか専攻している人が読んだら頭おかしなるで。
※もしそういう人から本当に苦情とかきたら 「ああ、当記事を読んで頭がおかしくなったんだな」 と反省することにいたします。
単回帰分析のやり方
まず、以下の様にAさんからQさんまでの勤続年数と、 1ヶ月あたりのミスの回数が書かれた表があります。
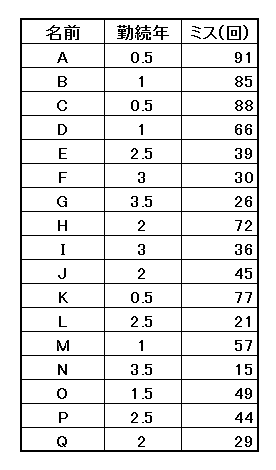
3.5年超がいないのは職場がブラックだから。
ざっと眺めてみると、勤続年数が長くなるにつれ、ミスが減っていることが分かります。 じゃあ、もし4年目の人がいたとしたら、彼の1ヶ月あたりのミス回数は、 一体どれくらいと予想できるのでしょうか。
それについて以下の様に求めます。
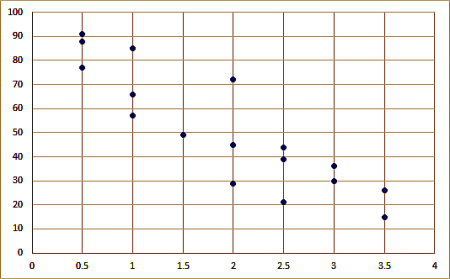
表を分散図にします。Excelでやって頂戴。
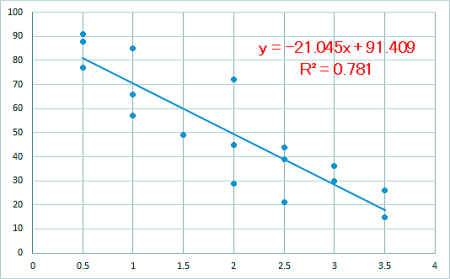
近似直線を引きます。分散図の点の1つを右クリックすれば引けます。
近似直線の式は、y=−21.045x+91.409の1次関数式なので、 x=4を入れると、y=7.229となります。
よって勤続年数4年目の人がいたとしたら、1ヶ月のミス回数は、 大体7回程度と予想できます。
さらに先に進むならば、 もし1回あたりのミスが1000円のロスを生んでいるとして、 従業員の月給をアップして長く働いてもらうことが必要になるといった、
給与アップ額とミスによる失われる額の関係から一番経済的効果のある額を求めたり、 そういうことをすれば良いんじゃないでしょうか。
解説
単回帰分析の簡単な例を挙げると、ざっとこんな感じでございます。
適当に解説していくと、まずグラフにある「R^2」ですが、 これは分散図の各データが、どれだけ近似曲線に沿っているかを 示す値です。
何で2乗なんだと思われるかもしれませんが、 近似直線を決定するのに「最小二乗法」が使われているということ、 分散は各データと平均の差の2乗だということ位が頭に入っていればOKですこんなの。 どっちみにExcelが勝手に算出してくれるし。
それより重要なのが、R^2の値が0.5以上だとその近似直線(曲線)はまあ妥当ということなので、 覚えるならこっちを覚えておきましょう。
また、単回帰分析があるなら重回帰分析はないのか、 と思われるかもしれませんが、 変数が複数存在する重回帰分析というのもあります。
しかし、そんなの職場でやったら説明する方も訳が分からなくなるし、 そもそも私はやったことないので記事に書くことできないしで、 興味ある方は統計のサイトでも見て勉強してください。
私は使わない
そんなわけで、単回帰分析とは、過去のデータを元にして先のことを予測する、 といったものでございました(本当は違うかもしれないけど)。
この「過去のデータから未来を予測する」というのは、
他人を騙す説得するには効果的な手段なのですが、
これを自分の人生に適用してしまうのは非常に危険であり、 「過去がこうだったから未来もこうだろう」 「統計的に、確率的にこうだから将来こうだろう」などという思い込みは、 人生をつまらなくする思い込みの1つであると私は考えます。
だいたい過去の状況、統計や確率
「東大の合格者は7割が現役」 「E判定で合格する確率は1割未満」 「受験生の9割以上が10月時点の成績で合否が決まった」
とかそういうのを信じていたら、 私は東大にすら合格しなかったではありませんか。
なので読者の皆様におかれましては、こんな統計や確率といった数字なんかに騙されず、 過去に振り回されたりせず、 自身の直感と可能性を信じて生きていただきたいと願っております。
何か「他人には食わせるが自分は食べない」という、 某食品メーカーの社長みたいなダブルスタンダードですが、 こういう数字を盲信している人がいるのも事実だし、 信じている人に対して使用すれば良いと思います。
生きる上で大変ためになる記事一例
引き寄せに関する大変素晴らしい記事一例
...